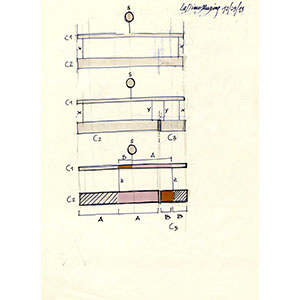
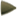The principle of the lever according to Galileo
Galileo returned to this proof at the beginning of book two of Archimedes' Quadrature of the Parabola. The assumption is the balancing of a cylinder suspended at its central point. Once divided into two unequal parts, these parts must be suspended from their respective central points to achieve balance. In the two positions, the weights are held once by the cords at the ends and then by the cords at the centre. In this latter case, the arms from which they hang are inversely proportional to the weights of the two balanced cylinders. For this reason, the two parts are linked to another cylinder, in turn suspended from its centre. The principle demonstrated here is that the system remains balanced if both spaces A and D and spaces B and C are respectively equal. Finally, the system remains balanced if the two segments of the cylinder are replaced with objects of a different shape but the same weight.