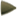Regular solids find their continuation in Archimedes' polyhedrons, which come in a wide range of forms. These include polyhedrons with faces that are regular polygons of two or more types and homogeneous vertexes. They were linked to Archimedes by the testimony of the 4th-century mathematician Pappus of Alexandria, who speaks of "the solids, thirteen in number, which were discovered by Archimedes." Even in the presence of the stated conditions, this family generally excludes prisms and antiprisms, which are infinite in number. Moreover, two of these figures (the snub cube and the snub dodecahedron) have specular non-equivalent images and so we sometimes speak of fifteen Archimedean solids.